Fredrick Grover’s invaluable tome is essential for partial inductance calculations.

Inductance is probably the most confusing topic in signal integrity, yet one of the most important. It plays a significant role in reflection noise, ground bounce, PDN noise and EMI. Fortunately, the definitive book on inductance, originally published in 1946 by Fredrick Grover, is available again.

After two printings in the 1940s, Grover’s Inductance Calculations was out of print by the mid 1980s. It was just reprinted this year and is available from Amazon in paperback (amazon.com/Inductance-Calculations-Dover-Books-Engineering/dp/0486474402/ref=sr_1_1?ie=UTF8&s=books&qid=1260191720&sr=8-1) for a very low price.

Motors, generators and RF components experienced a period of high growth in the 1940s. At their core were inductors, and being able to calculate their self- and mutual-inductance using pencil and paper was critical. (Keep in mind this predated the use of electronic calculators.) While many coil geometries had empirical formulas specific to their special conditions, Grover took on the task of developing a framework of calculations that could be applied to all general shapes and sizes of coils.

While Grover does not explicitly use the term, what he calculates in his book are really partial inductances, rather than loop inductances. A raging debate in the industry today is about the value of this concept. Proponents say it dramatically simplifies solving real-world problems and is perfectly valid as a mathematical construct. You just have to be careful translating partial inductances into loop inductances when applying the concept to calculate induced voltages. Opponents say there is no such thing as partial inductance; it’s all about loop inductance, and if you can’t measure it, you should not use the concept. There is too much danger of misapplying the term.

I personally am a big fan of partial inductance, and use it extensively in my book, Signal and Power Integrity – Simplified. It eases understanding the concepts of inductance, and highlights the three physical design terms that reduce the loop inductance of a signal-return path: wider conductors, shorter conductors, and bringing the signal and return conductors closer together. Most important, partial inductance is a powerful concept to aid in calculating inductance for arbitrary shaped conductors.

Inductance is fundamentally the number of rings of magnetic field lines around a conductor, per amp of current through it. In this respect, it is a measure of the efficiency for which a conductor will generate rings of magnetic field lines. To calculate the inductance of a conductor, it is a matter of counting the number of rings of field lines and dividing this by the current through the conductor. Counting all the rings surrounding a conductor is really performing an integral of the magnetic field density on one side of the conductor.

Literally everything about the electrical effects of interconnects stems from Maxwell’s equations. Grover starts from the basic Biot-Savart Law, which comes from Ampere’s Law and Gauss’s Law, each, one of Maxwell’s equations, and derives all his approximations. The Biot-Savart Law describes the magnetic field at a point in space from a tiny current element.

Using this approach, Grover is able to calculate the magnetic field distribution around a wide variety of conductor geometries and integrate the field (count the field lines) to get the total number of rings per amp of current. Using clever techniques of calculus, he is able to derive analytical approximations for many of these geometries.

The most commonly used approximation is for the partial self-inductance of a long, straight rectangular conductor, such as a lead frame in a QFN package or a connector pin. He calculates it as:

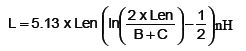
where
L = the partial self-inductance in nH
B, C are the thickness and width of the conductor cross section in inches
Len = the length of the conductor in inches.

For example, for a 1˝ long lead, 0.003˝ thick and 0.010˝ wide, the partial self-inductance is 23 nH. This is roughly 25 nH per inch, or 1 nH/mm, which is a common rule of thumb for the partial self-inductance of a wire.

If you deal with connectors, packages, vias, board discontinuities or odd-shaped transmission lines, and need to estimate the loop inductances of non-uniform sections, Grover’s book is a great resource. You will have a great collection of inductance approximations at your fingertips. It is well worth the low price.

Dr. Eric Bogatin is a signal integrity evangelist with Bogatin Enterprises, and has authored six books on signal integrity and interconnect design, including Signal and Power Integrity – Simplified, published in 2009.